Exponential Form

The exponential form is an easier way of writing repeated multiplication involving base and exponents. For example, we can write 5 × 5 × 5 × 5 as 5 4 in the exponential form, where 5 is the base and 4 is the power. In this form, the power represents the number of times we are multiplying the base by itself.

How to Write in Exponential Form?

To write numbers in exponential form, we need to express them raised to certain powers of their prime factors as shown in the following examples:

• 8 = 2 × 2 × 2 = 2 3 . Therefore, the exponential form of 8 can be expressed as 2 3
• 72 = 2 × 2 × 2 × 3 × 3 = 2 3 × 3 2 . Therefore, the exponential form of 72 can be expressed as 2 3 × 3 2
• 121 = 11 2 . Therefore, the exponential form of 121 can be expressed as 11 2

These are the exponential forms of the corresponding numbers. When it comes to representing numbers, there are three forms in which we can do that. Those are exponential form, factor form, and standard form. Any number can be represented in all three forms. Let us understand it in detail through the table given below:

Exponential Form to Logarithmic Form

An expression written in the exponential form can be easily converted to logarithmic form by using a simple formula: If e a = b, then \(log_b\) = a. Let us understand this conversion with the help of an example. Convert 5 3 =125 to log form. By equating it with the formula given above, we can say that, here, b = 125, a = 3, and e = 5. So, the logarithmic form is \(log_125\) = 3.

Logarithmic to Exponential Form

Now, let us understand how to convert logarithmic to exponential form. The same formula will be applicable to this also. If \(log_b\) = a is given, this implies, e a = b. Let us take an example. Convert \(log_100\) = 2 to exponential form. If we equate this to the above formula, we get b=100, a=2, and e=10. So, the exponential form will be 10 2 = 100.

Exponential Form to Radical Form

The conversion of an expression from exponential form to radical form is done by using the formula: x m/n = n √x m . Radical denotes the √ symbol which is used to represent nth roots. To convert an exponential form to a radical form, the denominator of the exponent will shift to the left of the radical sign, and the numerator will be the power of the radicand. It is only possible for fractional exponents. If the exponent is a whole number, then the radical sign is not used as it is only used to represent roots. For example, 2 3/5 can be represented in radical form as 5 √2 3 .

Observe the figure given below to understand the exponential form to radical form conversion formula along with an example.

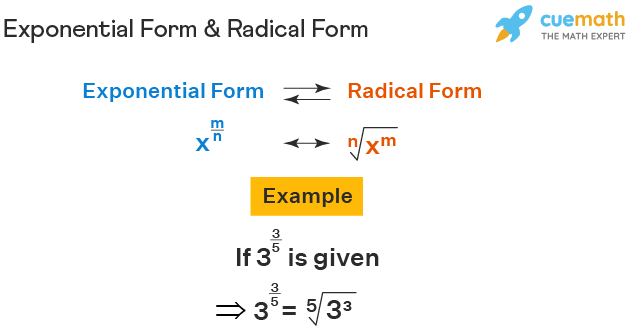
Similarly, we can also convert a radical form to an exponential form. For example, if 3 √3 is given, it means in the exponent form, the numerator of the power will be 1 and the denominator will be 3. So, 3 √3 = 3 1/3 .

Standard Exponential Form

If very large numbers or very small numbers are given, then it is better to use the standard exponential form to represent them. For example, it is difficult to make sense of the number 2030000000000000, but it will be easier if we write it in standard form as 2.03 × 10 15 . It is also known as a scientific notation to write numbers. To write a number in standard exponential form, we follow the steps given below:

• Step 1: Count the number of trailing zeros in the number.
• Step 2: Use the beginning of the number and write the digits from the left till the last non-zero digit followed by a 10 raised to power which is equal to the number of trailing zeros.
• Step 3: Place a decimal point after the first digit from the left side and add the number of decimal places created to the power of 10. For example, in the example written above, if we place a decimal point after 2, then two decimal places will be created in the number 2.03. So, we will add 2 to the existing power of 10. The power of 10 was 13 as there were 13 trailing zeros, but now it will become 15.
• Step 4: Therefore, the standard exponential form of the number 2030000000000000 is 2.03 × 10 15 .

Here, it is important to note that the decimal number written in the standard exponential form will always be greater than 0 and less than 10.

☛ Related Topics

• Exponential Functions
• Exponential Equations
• Exponent Rules

Exponential Form Examples

Example 1: Write 2000 in exponential form. Solution: To write 2000 in the exponential form, we have to find the prime factorization of 2000. The prime factorization of 2000 is 2 × 2 × 2 × 2 × 5 × 5 × 5. It means 2000 = 2 4 × 5 3 .

Example 2: Convert \(log_16\) = 2 in exponential form. Solution: The formula to convert logarithmic to exponential form is, if \(log_a\) = b, this implies, e b = a. It means \(log_16\) = 2 can be written as 4 2 = 16. Therefore, 4 2 = 16 is the required answer.

Example 3: Convert the following numbers written in standard form to exponential form. a) 1024 b) 350 Solution: To write these numbers in exponential form, we will use the prime factorization method. a) 1024 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2 10 b) 350 = 2 × 5 × 5 × 7 = 2 1 × 5 2 × 7 1

Indulging in rote learning, you are likely to forget concepts. With Cuemath, you will learn visually and be surprised by the outcomes.